Dynamics on networks and beyond team
We live in an interconnected world, where “basic” units interact each other to produce unexpected emergent behaviours. Our society is for instance, the result of the interaction of many agents, we the human beings, that exchange information, news, opinions, likes, etc., but also viruses. To a larger scale, the societies can be considered as agents interacting each other on a global stage, by exchanging goods to create the global economy, or by fighting each other and thus leading to conflicts and wars.
Our brain is made of about 100 billions of cells, i.e., the neurones, connected through even more synapses (millions of billions) allowing the signals to pass from one neurone to the others, and thus allowing us to think, act, remember, … Finally, our body is made by about 30 thousand billions of cells, basic blocks that determine our behaviour, via synchronised processes, resulting from the exchanges among the cells. The cells are also organised into tissues and organs and so on to allow us to be alive.
The following questions thus straightforwardly arise. Is it possible to understand the behaviour of a society ? How to understand the brain functioning, to distinguish between its regular or irregular behaviour (disease) and thus control it to reduce / remove the unwanted behaviour ? Can we determine the behaviour of (part of) the human body? A reductionist or mean field approach, may fail to sufficiently well describe the whole system, indeed the resulting global behaviour is not easily ascribed / predicted from the behaviour of each single unit. How would it be possible from the behaviour of a single human to extract the behaviour of a society? Or, does a neurone have memory? To cope with these issues, network science, dynamical systems and complex systems offer a reliable alternative approach.
Current projects
Turing instability on networks and beyond
A blossoming of regular spatio-temporal patterns can be observed in Nature. These are the signature of self-organised processes where ordered structures emerge from disordered ones. Very often, the interaction among the microscopic units, by which the system is made of, can be modelled by means of reaction-diffusion equations that describe the deterministic evolution of the concentrations of the involved quantities, both in time and space, the latter being often a discrete one, e.g., a complex network. Spatially homogeneous equilibria of a reaction-diffusion system may undergo a symmetry breaking instability, when subjected to a heterogeneous perturbation, eventually driving the system towards a patchy, i.e., spatially heterogeneous, stationary or oscillatory solution, as firstly explained by Turing in the 50s and corroborated experimentally almost four decades later.
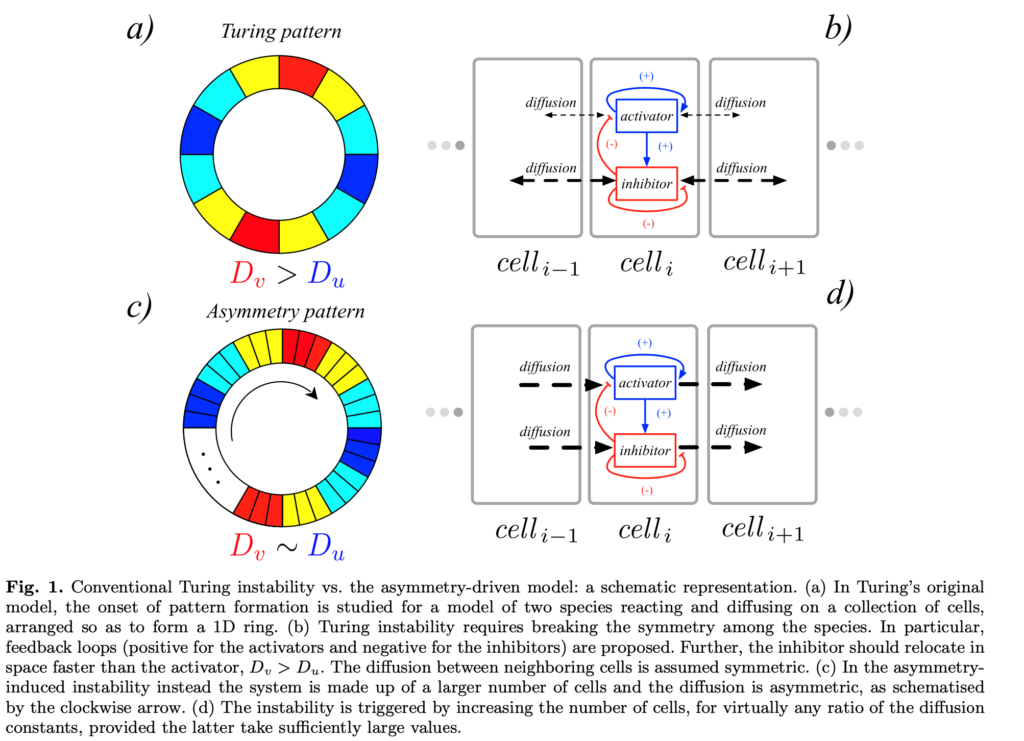
Nowadays, the Turing instability phenomenon stands for a pillar to explain self-organisation in Nature and its applications go well beyond the original framework of the morphogenesis or chemical reaction systems. Our goal is to study the onset of the Turing instability, both on networks and higher-order structures, under different conditions to be able to reduce the gap between the theory and the experiments.
Most relevant publications:
- Turing patterns on discrete topologies: from networks to higher-order structures
- Turing patterns in systems with high-order interactions
- Finite propagation enhances Turing patterns in reaction-diffusion networked systems
- Patterns of non-normality in networked systems
- Theory of Turing Patterns on Time Varying Networks
- Pattern reconstruction through generalized eigenvectors on defective networks
Long-range dynamics
We live in an interconnected world where complex patterns spontaneously emerge from the intricate web of nonlinear interactions existing between the basic units by which the system under study is made of. These emergent structures can be found in the synchronised activity of neurones, resulting from the exchange of electrochemical signals via synapses, as well as the geometric visual hallucinations products of the retinocortical map linking the retina and the striate cortex. Such self-organised structures can also manifest in groups of fireflies that flash at unison, each one observing the behaviour of their close neighbours. Or they can materialise as the striped or spotted motifs on the skin of the zebrafish Danio rerio, due to the long-range interactions between melanophores and xantophores, without requiring diffusion nor any kind of cell motion.
The latter phenomena, as well as many other ones modelled within a similar framework of local reactions and long-range interactions without displacement, cannot be ascribed to a Turing instability, a paradigm for pattern formation. Indeed the latter requires a diffusive process, whereas the common key factor linking the above examples is the immobility of the reacting species and the existence of a web of long-range interactions due to some signal propagation.
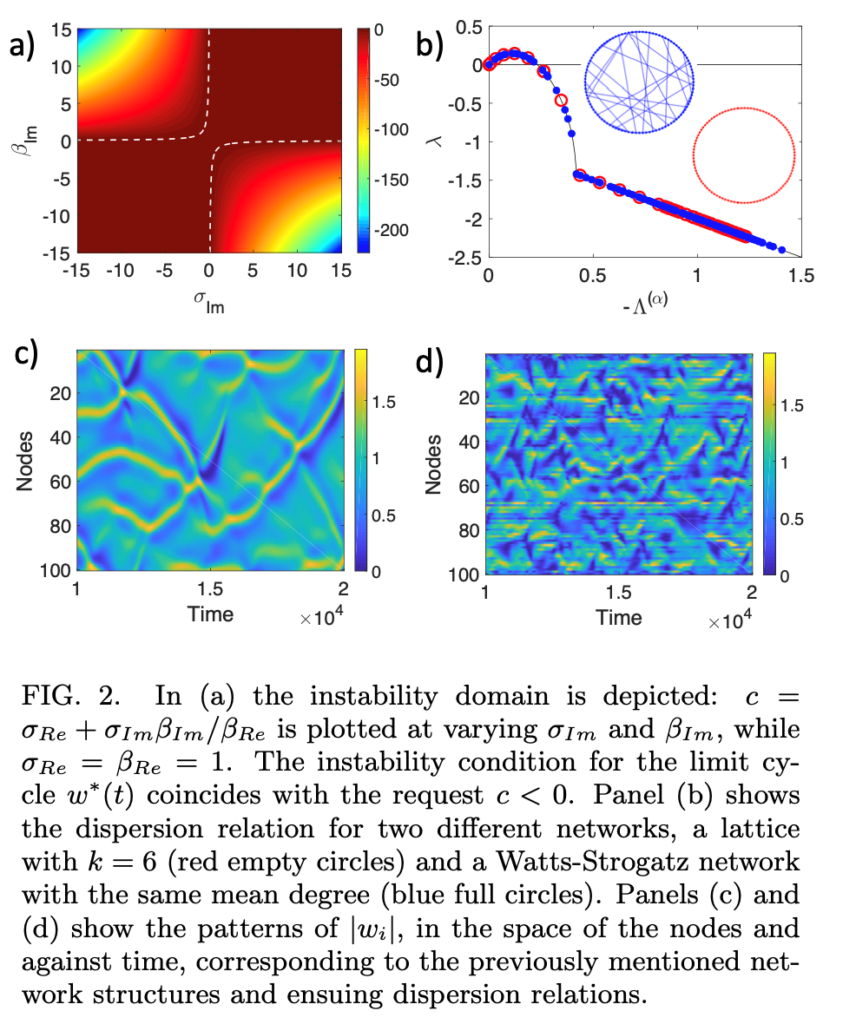
Most relevant publications:
- Generalized patterns from local and non local reactions
- Non-reciprocal interactions promote diversity
Dynamical systems on hypergraphs and simplicial complexes
Network science has proved successful in describing many real-world systems, which, despite inherent differences, share common structural features. Scholars have proved that dynamical processes and hosting networks are indissolubly entangled with the ensuing patterns that reflect in fact the complex topology of the supports to which they are anchored.

Networks constitute abstract frameworks, where pairwise interactions among generic agents, represented by nodes, are schematised by edges. Stated simply, two agents are connected if they interact. Hence by their very first definition, networks encode for binary relationships among units. This descriptive framework is sufficiently accurate in many cases of interest, although several examples exist of systems for which it holds true just as a first order approximation.
The relevance of high-orders structures has been indeed emphasised in the context of functional brain networks, in applications to protein interaction networks, to the study of ecological communities and co-authorship networks.
Despite the diversity of the above models, they all have in common the fact that the interactions among individuals, being them neurons, proteins, animals or authors, cannot be reduced to binary exchanges. The group action is the real drive of the dynamics. Our goal is thus to study dynamical systems and their properties, taking into account the high-order interaction modelled with hypergraphs or with simplicial complexes.
Moreover simplicial and cell complexes allow to study topological signals, namely dynamical variables associated with higher-order structures, such as nodes, links, faces. We are thus interested in studying the emergence of Turing patterns as well as Global Topological Synchronization in this novel framework.
Most relevant publications:
- Topology shapes dynamics of higher-order networks
- Random walks and community detection in hypergraphs
- Dynamical systems on hypergraphs
- Random walks on hypergraphs
- Global topological synchronisation on simplicial and cell complexes
- Global Topological Dirac Synchronization
- Diffusion-driven instability of topological signals coupled by the Dirac operator
- Impact of directionality on the emergence of Turing patterns on m-directed higher-order structures
Random walks
From social systems and the World Wide Web to economics and biology, networks define a powerful tool to describe many real-world systems. Over the past 20 years of network science, many interacting systems with different functions were shown to exhibit surprisingly similar structural properties, at different scales. Interestingly, the complex architecture of real-world networks was found to significantly interfere with the dynamical processes hosted on them. As a consequence, properly tailored dynamical processes are now routinely employed to extract information on the a priori unknown structure of the underlying graphs architectures.

Linear dynamics and specifically random walks constitute a simple although powerful tool to extract information on the relational structure of interacting systems. In particular, random walks on complex networks have been proven useful to compute centrality scores, finding communities and providing a taxonomy of real-world networks. In the simplest case, at each time step, a walker jumps from the node where it belongs to one of its adjacent neighbors, traveling across one of the available edges, chosen at random with uniform probability. Our goal is to explore other possible mechanisms ruling different random walk processes as well to define random walk on substrate beyond the networked ones.
Most relevant publications:
- Random walks and community detection in hypergraphs
- Random walks on dense graphs and graphons
- Nonlinear walkers and efficient exploration of congested networks
- Random walks on hypergraphs
- Hopping in the Crowd to Unveil Network Topology
- Self-segregation in heterogeneous metapopulation landscapes
- Emergence of power-law distributions in self-segregation reaction-diffusion processes
- Multigraph reconstruction via nonlinear random walk
Synchronisation of interconnected systems
Synchronisation is one of the key mechanisms responsible for self-organisation and emergence in living organisms as well as in technological products. For instance, regular and periodic activity emerging from the collective behaviour of a set of interacting agents, has been noted to be crucial for the operation of many processes in living organisms. A prime example are the firing patterns of neuronal populations that form the basis of brain activity and their coordination among distributed mesoscopic neuronal populations that ultimately controls our behaviour with an impressive and somehow mysterious accuracy. It is therefore not surprising that defects or hypersynchronisation in neural firing patterns can lead to a host of neurological and psychiatric pathologies such as schizophrenia, Alzheimer’s disease, Parkinson’s disease and epilepsy. It is thus of main importance to be able to act on the system and to control the synchronised state, to reduce or suppress the undesired behaviour.
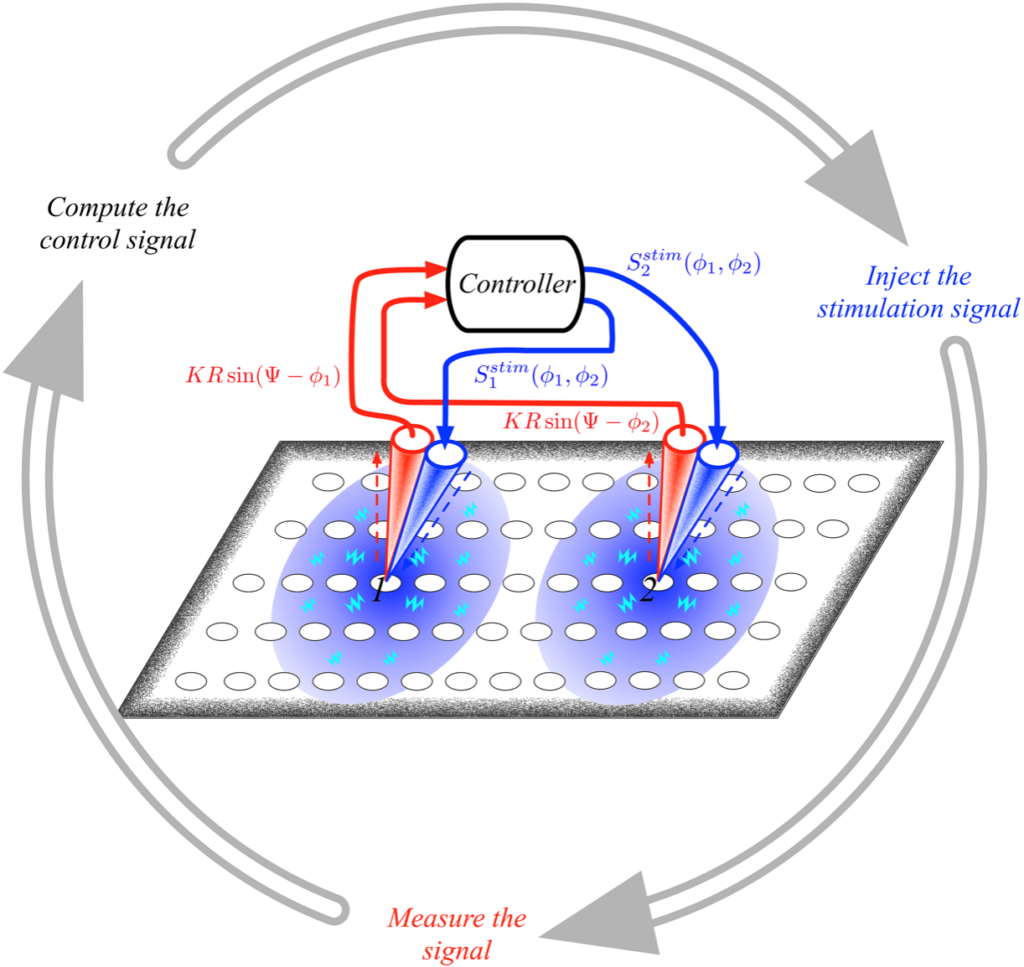
Our goal is twofold, from one side we lay down the basis for a theory of synchronisation in interconnected general systems to study the emergence or suppression of the latter. On the other hand we are interested in practical applications of the developed theory, with particular attention to the field of brain dynamics using reliable networks models for the brain.
Most relevant publications:
- Synchronization Dynamics in Non-Normal Networks: The Trade-Off for Optimality
- Synchronisation induced by direct high-order interactions
- A minimally invasive neurostimulation method for controlling abnormal synchronisation in the neuronal activity
- Using Hamiltonian control to desynchronize Kuramoto oscillators
- Hamiltonian control to desynchronize Kuramoto oscillators with higher-order interactions
- Strategy to control synchronized dynamics in swarmalator systems
- Synchronization in adaptive higher-order networks

